Project: Formalistic Philosophy

Formalistic philosophy is an attempt to describe philosophical principles, theorems, and concepts with a formal diagramming language. The formalism (graphical notation) consists of the following basic elements:

• Entities, or philosophical/metaphysical concepts (subject, object, matter, substance, cause, etc.). Entities are rendered as simple graphical icons or symbols.
• Attributes that further describe or define the entities. Attributes are associated with entities. Attributes are rendered either as letters that are added next to the entity symbol or as a graphical modification of the entity.
• Relationships that define interactions or associations (conceptual or physical) between entities. Relationships are rendered as directional lines (arrowhead at either end). Relationships can have the following attributes: roles, kinds, direction, intentionality, and others.
• Definition variance is rendered as a number added to the entity icon. Each number is a different definition that need to be written out explicitly in an attached note.
• References are rendered as a capital letter "R" next to the entity or entity construal. The actual reference is written in parentheses next to the "R", e.g. R(Kant CPR, A320).
• Derivation is a tracing relationship and shows how certain entities are developed or derived throughout various entity construals. The same entity can be reused in many different entity construals. The relationship is rendered as a dotted arrow line back to the previous occurrence. The modificator is '[relates]'.
• Modificators (qualifiers, ascriptors) are attributes that modify, enhance, or further qualify/define an entity or relationship. Modificators are rendered as text between square brackets and are used on top of relationships or entities.
• Dependencies are rendered as solid line with an arrow pointing to the entity on which it is dependent and the modificator '[depends]'. 
• Entity construals: entities can be used to build a postulate or axiom (basic, self-evident principle, assumption). One or more postulates/axioms constitute a theorem or are part of an argument (syllogism, premises). One or more theorems are organized into a theory, or one or more arguments are organized into a system.

The idea behind this philosophical formalism is to visualize abstract and complex metaphysical ideas and principles. It also allows to build theorems or even whole systems of thought by using entities and entity clusters (building blocks) to logically and graphically derive a philosophical theory.

At the time of writing, this idea of a formalistic philosophy is not yet a complete formalism but just a first draft of a final definition. I will continue developing this formalism and add more symbols and constructs to it. I know that this is a very amibitious project and it will take time and experience to see if this idea pans out and can be applied in practice at all.

Notational Entities

Entity	Name	Attributes
	object	real, ideal, subjective, objective, physical, cognitive, mental, etc.
	subject	logical, epistemological, ontological, psychological
	substance
	accident	primary, secondary
	form
	matter
	time	past  present  future
	space	absolute, relative
	finite, limited, constrained
	infinite, unbound, free
	world, universe, cosmos, evolution
	whole, unity, totality
	part
	cause
	effect
	truth	logical, factual
	falsity, contradiction, inconsistency
	essence
	being, beingness, 'Dasein'
	existence, life
	knowledge, self-consciousness, contemplation, reflection
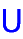
	universal, generic
	particular, individual, concrete, specific
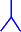
	principle, axiom
	process

Entity Construals (Examples)

Postulate: The Whole is more than the sum of its Parts.



The relationship between the two entities can be modified by attributes (modificators), such as the 'greater than...'.

Postulate: The existence of an individual form (thing, living being, etc.) can be defined as the integration of the two aspects of essence and being.



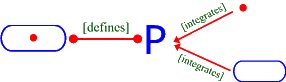
In this example two modificators are applied to the relationships: the '[defines]' and the ['integrates]'. The letter 'P' represents a particular thing or being as opposed to a universal concept.

Postulate: The principle of sufficient reason says that nothing exists without a reason for its being.



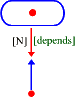
Leibniz' principle can be represented simply as the entity of cause pointing to existence. The '[depends]' modificator represents that existence is dependent on something that caused it. The '[N]' modificator further defines this dependency relationship as necessary.

---